デイレクレ分布の直感的な説明

注意事項

この記事は前もって確率密度と正規分布関数、積分微分の知識がある事を前提としています

確率密度関数

導入

今回はデイレクレ分布について直感的な説明をしようと思います

デイレクレ分布の利点を言いますと、この確率密度関数は汎用性が高く（正規分布には劣りますが）更には正規分布よりも融通がきくという事です

下の図をご覧にならばハッキリ分かると思います

(1) (2) (3)

f:id:phonetic:20180723142838p:plain — 図3

f:id:phonetic:20180723142904p:plain — 図3

上の図は、それぞれ正規分布に従う確率分布の乱数(1)とデイレクレ分布に従う確率分布の乱数(2),(3)です。(2)と(3)の違いは、図の下にあるalphaとbetaという値の違いです。これは、デイレクレ分布の式のα、βの事ですが、ここで説明するとややこしくなってしもうので、今は「この二つの値を変えると確率変数の分布が変わるんだな」ぐらいに思って大丈夫です（ちゃんと後で説明します）。それぞれの発生する乱数の範囲は「0.0~1.0」の範囲にします。何故かというと、デイレクレ分布の公式での確率変数の範囲が[0.0~1.0]だからです

(話は若干ずれますが)勘のいい読者はここで疑問に思うでしょう！発生する乱数の範囲が[0.0~1.0]しかとれないなら、正規分布の方がよほど便利だ！何故なら、正規分布は無限の範囲の乱数を派生出来るからです。しかし、

「0.0~1.0」までの乱数が発生できれば全ての範囲の連続な乱数が生成できます。例えば、0.0~50.0までの乱数生成したい場合は「0.0~1.0」の範囲の乱数に50掛けれ大丈夫ですし、[-25.0, 25.0]の乱数を発生したい場合はこんどは「0.0~1.0」の範囲の乱数で0.5を引いて15を掛ければいいのです。勿論、[-inf +inf]の範囲は発生する事が出来ないのですが、それを話すと話が複雑になるので割愛します。

話を元に戻しましょう。図2（1）の正規分布乱数が中心に集まるのは（正規分布の関数を見れば分かるように）、正規分布ではどのようにパラメータ（分散と平均）を変えようとも「平均に集中して集まる乱数」しか作れません。それもそのはず、正規分布の確率密度関数は平均値が最高値になるように作られてるからです。図2（2)のような「両辺に集中して真ん中が疎らになる」ような乱数は生成できません。その辺、デイレクレ分布はパラメータを変える事で(2)のような「両辺に集中する分布」も(3)のような「真ん中に集中する分布」も作れるのです。

また、パラメータを変更する事によってこんな分布も作れます。

f:id:phonetic:20180723151635p:plain — 図2

確率変数の分布が右に傾いていますね。このように、デイレクレ分布ではパラメータによっては右に傾いた分布だって出来るのです。

このように、デイレクレ分布は「平均値に集中する」正規分布よりも多種多様な分布を生成できる為、「正規分布よりも融通のきく」確率分布となるのです

2.デイレクレ分布に関する説明

2.1 デイレクレ分布の公式に関する説明

それでは、いよいよデイレクレ分布の公式に関する説明をしましょう

話を簡単にする為に、最初に1次元の場合の話をしましょう

前章でもお話しましたが、1次元のデイレクレ分布をベータ分布と言いますが、ここでは話を簡単にする為に二次元デイレクレ分布と呼びます。二次元デイレクレ分布の公式は以下のようになります。

$Beta(\mu|\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\mu^{\alpha-1}(1-\mu)^{\beta-1}$ ①

一番最初の項( $\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}$ )は正規化項と言われるものです。ご存知の通り、確率密度関数の全積分した後の値は1にならなければいけません。正規項の右辺の変数「 $\mu^{a-1}(1-\mu)^{b-1}$ 」を積分しても1にはなりません。その為、正規化項をかける事によって、①式の「 $\int Beta(\mu|\alpha,\beta)dx$ 」が成り立つのです。正規化項の詳しい説明と導出はこちらのサイトを参考できればなと思います。

mathtrain.jp

さて、ベータ分布の話に戻りましょう。前章で説明したαとβがでてきましたね。今回はこの公式を使い、色々なベータ分布を計算します。

まずはα > 1, β > 1(ここではα = 15, β = 15)の式をplotしてみましょう。

用いる言語はpythonです。scipy ライブラリのscipy.stats.beta.pdfを使うとプロットできます(

scipy.stats.beta — SciPy v1.1.0 Reference Guide

)。結果は以下のようになります。

f:id:phonetic:20180723201541p:plain — 図3

正規分布みたく、真ん中が突起した確率分布になりましたね。このように、α,βが1より大きい時の分布は真ん中がふっくらした分布となるのです。勿論、この分布で発生する乱数は真ん中に集中した乱数になるでしょう。図2(2)の乱数はこのような分布に従ってます。（(pythonではscipyライブラリのscipy.beta.pdf()という関数で1次元乱数を発生させる事が出来ます)。

次に、0 < α < 1, 0 < β < 1(α = 0.1, β = 0.1を例に)の関数をplotしてみましょう。

f:id:phonetic:20180723202334p:plain — 図4

今度はブーメランみたいに両端が極端に跳ね上がっている関数になりましたね（今回は確率変数の範囲が0.0から1.0だと仮定したが、任意の範囲が知りたい方は付録B*を参照）。確率は確率密度関数の指定範囲の積分で決まりますので、上の図のように確率変数の範囲を一定に選ぶと、両端に集中する確率分布になります。つまり、両辺に乱数が散らばる確率分布となるのです。

勿論、両端が無限大の関数は積分出来るのかという問題が残りますが、そこはルベーグ積分の説明をしてる別のサイトや参考書に任せます。

2.2 何故、デイレクレ分布の式はパラメータを変えると分布が変化するのか

それでは、何故このような現象が起こるのでしょう。

2.2.1 （α、β）が1より大きい場合

まずはパラメータ（α、β）が1より大きい場合を考えましょう。そして、α = βである事を過程します。分数の累乗の性質を考えてみましょう。

ここで高校での数学の授業を思い出して下さい。冪関数 $y = x^a$ はa > 1, 0 <= x <= 1の時には以下の性質が成り立ちます。

$x^{a}$ > x 性質(1)

(wikipediaより引用)

この性質がどう役に立つかは再び①の1次元デイレクレ分布の公式を見れば分かります。まずは簡単な[α = β, α > 1, β > 1]の場合を考えてみましょう。すると、①式は以下のようになります。

となります。上の式の $\frac{\Gamma(\alpha, \alpha)}{\Gamma(\alpha)\Gamma(\alpha)}$ の部分は定数ですので、 $(\mu(1-\mu))^{\alpha - 1}$ の部分を見てみましょう。冪を外すと $\mu(1-\mu)$ となります。これはは $\mu = 1 / 2$ の時に最大値に達っする二次関数になります。α-1 > 0次に冪を見てみましょう。今回はα > 1なので冪は(α-1 > 0)となります。よって性質(1)より、 $(\mu(1-\mu))^{\alpha - 1}$ < $\mu(1-\mu)$ となります。 $(\mu(1-\mu))$ の値が小さいほど（つまり $\mu$ の値が0か1に近づく程）急激に小さくなります。また $x^a$ はxを[0, 1]の範囲と指定してαが定数の時、xが小さくなるにつれて急激に小さくなります。この問題を押し込むと、 $(\mu(1-\mu))^{\alpha - 1}$ の関数の両端の部分（つまり、 $\mu$ が0か1に極端に近い時）、元々の $(\mu(1-\mu))$ 関数の値よりも更に小さくなるのです。

f:id:phonetic:20180724112520p:plain — 図5

f:id:phonetic:20180724183529p:plain — 図5

図5の右側の図が $(\mu(1-\mu))^{\alpha - 1}$ で左が $(\mu(1-\mu))$ です。右側の黒線より外側の部分が左の図形より凹んでます。先程も話したように、αが1よりも大きい為、両端の小さい値が極端に潰れるのです。

それでは、αの値が変化する事によって関数のグラフがどう変わるかを見てみましょう。

今度はαが変数なので、正規化項を無視する訳にはいかなくなりましたが、今回も一つずつ謎を解決していきましょう。

まずは $(\mu(1-\mu))^{\alpha - 1}$ の部分ですが、冪が0より大きい冪関数の性質により、

$(\mu(1-\mu))$ < 0なので（0 < $\mu$ < 1より）

$\alpha_1$ < $\alpha_2$ の時

$(\mu(1-\mu))^{\alpha_1 - 1}$ > $(\mu(1-\mu))^{\alpha_2 - 1}$

が成り立ちます。つまり、αの値が大きくなると $(\mu(1-\mu))^{\alpha - 1}$ の値も小さくなります。言い換えると、αの値を大きくすると真ん中の山が大きくなるのです。これで、前節で話した「αを大きくすると、より真ん中に集中する分布となる」現象の説明ができます。

f:id:phonetic:20180725122655p:plain — 図6

( $(\mu(1-\mu))^{\alpha_1 - 1}$ > $(\mu(1-\mu))^{\alpha_2 - 1}$ )の関係を表した図で、赤い線がα=16の時の $(\mu(1-\mu))^{\alpha - 1}$ のグラフで青い線がα=16の時のグラフです)

これで全てが解決した.....はずですが、前述のとおり、まだ正規化項の話が残ってます。しかし、正規化項の問題もそこまで難しい話ではありません。正規化項とは分布関数の全積分を1にする為に公式に付け加えられた数です。つまり、αがどんなに変わろうともデイレクレ分布の全積分は「同じ1」になるのです。よって、( $(\mu(1-\mu))^{\alpha_1 - 1}$ のグラフ(図5)を全て「同じ積分結果の1」に調整するような係数を考えればいいのです。

それでは図5に戻りましょう。係数を掛けて「同じ積分結果」に変換する事を考えましょう。「積分結果1にする事」は「同じ積分結果」の関数に変形した後に、定数項を掛ける操作なので、「積分結果1にした」関数と大小関係は同じになります。よって、「同じ積分結果」にする事さえ分かれば「αの変化によってデイレクレ分布がどう変化するか」と同じ解を求める事が出来ます。同じ積分結果とは、同じ面積になる事なので、係数をかけて同じにするには赤いグラフ(α=16)の関数に1より大きい関数を掛けて増すか、青いグラフ(α=15)の関数に1より小さい正数をかけて小さくすれば大丈夫でしょう（ $\int{ax} = a\int{x}dx(aはxと無相関の関数)$ と言う性質を使った）。

f:id:phonetic:20180725122911p:plain — 図6

図6のような関数になるのです。赤い関数も青い関数も(図5)真ん中( $\mu$ = 0.5付近)の差が最も広がってる所は大きく変化します。かし、両端の差が小さくなってる部分では殆ど図ロ5と同じになります。大きな数ほど定数掛けた後に変化する幅が増えるからです。

2.2.1.2 $\alpha \neq \beta$ の場合

α < βの場合だけを考えましょう。（逆は対偶で解けるからです）

$Beta(\mu|\alpha,\beta) = \frac{\Gamma(\alpha, \beta)}{\Gamma(\alpha)\Gamma(\beta)}\mu^{\alpha-1}(1-\mu)^{\beta-1} = \frac{\Gamma(\alpha, \beta)}{\Gamma(\alpha)\Gamma(\beta)}\mu^{\alpha-1}(1-\mu)^{\beta + \alpha -\alpha -1} = \frac{\Gamma(\alpha, \beta)}{\Gamma(\alpha)\Gamma(\beta)}\mu^{\alpha-1}(1-\mu)^{\alpha-1}(1-\mu)^{\beta - \alpha}$

$= \frac{\Gamma(\alpha, \beta)}{\Gamma(\alpha)\Gamma(\beta)}(\mu(1-\mu))^{\alpha-1}(1-\mu)^{\beta - \alpha}$

となります。最後の式の左側は前と同じになります。唯一違うのが $(1-\mu)^{\beta - \alpha}$

の部分です。ここで $\mu$ は[0, 1]でβ-α > 0なので、減少する関数になります(1から0に減少します)。更に、冪関数の性質により、最初は急激に現象しますが、後からは緩やかに現象します(図7参照)。

f:id:phonetic:20180725135601p:plain — 図7

この関数を元の( $(\mu(1-\mu))^{\alpha_1 - 1}$ に掛けるとどうなるでしょう。図7から分かるように、右側が急激に減少してるので、元の左右対称（図5の右）のグラフの右側が潰れて左半分に傾く事なります。つまり、元々の関数の山が左へ移動する事になるのです。

f:id:phonetic:20180725140600p:plain — 図8

2.2.2 α , β <1の場合

今度はパラメータが1より小さい場合を考えましょう。この問題は一部の変更点を除いては2.2.1節と対して変わらないので、頭のいい人はここを飛ばして大丈夫です。とはいえ、この変更点が中々の曲者なので、私も念の為に説明する事にしました。

さて、パラメーターが小さい時には上に口が開いてるブーメランの形になると書きましたが、それは何故でしょうか。それは下の式の導出を見れば分かります（前と同じようにα = βを仮定）。

$Beta(\mu|\alpha,\beta) = \frac{\Gamma(\alpha, \beta)}{\Gamma(\alpha)\Gamma(\beta)}\mu^{\alpha-1}(1-\mu)^{\beta-1} = \frac{\Gamma(\alpha,\alpha)}{\Gamma(\alpha)\Gamma(\alpha)}\mu^{\alpha-1}(1-\mu)^{\alpha-1} = \frac{\Gamma(\alpha,\alpha)}{\Gamma(\alpha)\Gamma(\alpha)}(\mu^(1-\mu))^{\alpha-1} = \frac{\Gamma(\alpha,\alpha)}{\Gamma(\alpha)\Gamma(\alpha)}(\mu^(1-\mu))^{-(1 - \alpha)}= \frac{\Gamma(\alpha,\alpha)}{\Gamma(\alpha)\Gamma(\alpha)}\frac{1}{(\mu^(1-\mu))^{1 - \alpha}}$

$\frac{\Gamma(\alpha,\alpha)}{\Gamma(\alpha)\Gamma(\alpha)}\frac{1}{(\mu^(1-\mu))^{1 - \alpha}}$ -- ②

ここで $\frac{1}{(\mu^(1-\mu))^{1 - \alpha}}$ (③)の所を見てみましょう。基底部分の $\frac{1}{(\mu^(1-\mu))}$ の基底グラフは以下のようになります（理由は高校数学で解けるので割愛します）。

f:id:phonetic:20180726064518p:plain — 図9

更に1 - α > 0により、 $\frac{1}{(\mu^(1-\mu))}$ の元から小さい部分(図9の横軸の0.5付近)は急激に小さくなり、大きい部分(両端)はさほど変化しません。つまり、上の図形はさほど変化しないのです。更にαの値を1に近づけると、1 - αは0に近づく為、図9の関数のグラフは一様分布に近づくのです。

2.3 α < 1, β > 1の場合

ここは読者に推敲を委ねましょう。結論から言うと以下のようになります。

f:id:phonetic:20180726070228p:plain — 図9

ヒントを挙げるとすると、今までやってきたように冪が正の数になるように調整する事ですね。

0に近い方は無限に発散して、1に近い方は最終的に0に収まります。そして、αを1に近づけると関数は左に傾きが大きくなります。逆に、βを大きくすると関数は右に険しくなります。考え方としては（α > 1, β > 1）と(α < 1, β < 1)の両方を結合した感じですね。

2.43 多次元デイレクレ分布

さて、いよいよ多次元デイレクレ分布に入ります。まずは3次元から入ってみましょう。3次元は大抵の本では単体によって表されます。単体は簡単な概念なので、本来は説明がいらないはずですが、自分が苦労した経緯を考えると説明する必要があると思いますので、付録に回して説明しましょう。

さて、付録C*にもあるように、単体には重要な性質があります。それは、単体内の点xはその全ての座標点を足した数は1になると言う事です。式では以下のようになります。

x1 + x2 + ..... xn = 1 (全ての変数は単体上の点)

さて、これを見てピンと思い当たる事はないでしょうか。

そう、我々のデイレクレ分布の関数も同じく確率変数の和が0になるのです。だから、デイレクレ分布に基づいて発生した乱数は必ずやこの単体の中の座標で表す事が出来ます。

それぞれのパラメータを変えた結果が以下のようになります。考え方は基本、1次元と一緒です。

まずは、全てのパラメータが1より大きく等しい場合を考えます。そして、パラメータを調整してαとβで違う場合を導出すればいいのです。

3.2

それでは、デイレクレ分布を使った例を見てみましょう。

3.2.1 LDA

まずはLDAを説明したいと思います........とは言え、LDA自体はもの凄く複雑な体系なので、ここで全部説明する訳にはいけません。よって、ここでは概要とデイレクレ分布を説明する事にしましょう。

まず、LDAとはLatent Dirichlet Allocation(潜在的トピック解説)の略で、その名の通り、与えられた各単語がどのトピックに属するかを割り当てる一種の数理モデルです。ところが、人間の言葉は非常に難しく、一つの単語が必ずしも一つのトピックだけと関連するとは限りません。例えば、スイングと言う単語があります。

wikipediaより

スポーツ用語

野球・ソフトボール・クリケットなどでバットを振ること。スイング。「打撃 (野球)#スイングに関する用語」も参照。

ゴルフでクラブを振ること。スイング。

テニス・バドミントン・卓球などでラケットを振ること。スイング。

スイング (ボクシング) (en) - ボクシングのパンチの打ち方のひとつ。大きな弧を描きながら打つ、大振りのフック

スイング (ダンス) (en) - スウィング・ジャズに合わせたグループでのダンス。

音楽用語

スウィング (音楽) - ポピュラー音楽のリズムの一種。

スウィングする - ジャズにおいて、「スウィングする」という語は強いグルーヴ感を持った演奏に対する賞賛の辞として用いられる用語(上記で説明)。

スウィング・ジャズ - 大人数編成によるジャズの形態の一つ。「スウィング」というリズムの演奏を行っていたためだが、現在では他のリズムや他のジャンルも演奏される。

wikipediaのページから分かるように、この単語は「スポーツ」と「音楽」の両方のトピックを持ち合わせています。よって、正確にはldaの数理モデルによって割り当てられるのはその単語がそれぞれのトピックに属する「確率」なのです。同じく「スイング」の例を挙げますと、「スポーツ」というトピックに属する確率は60%, 音楽というトピックに属する確率は30%, それ以外が10%というような感じですね。

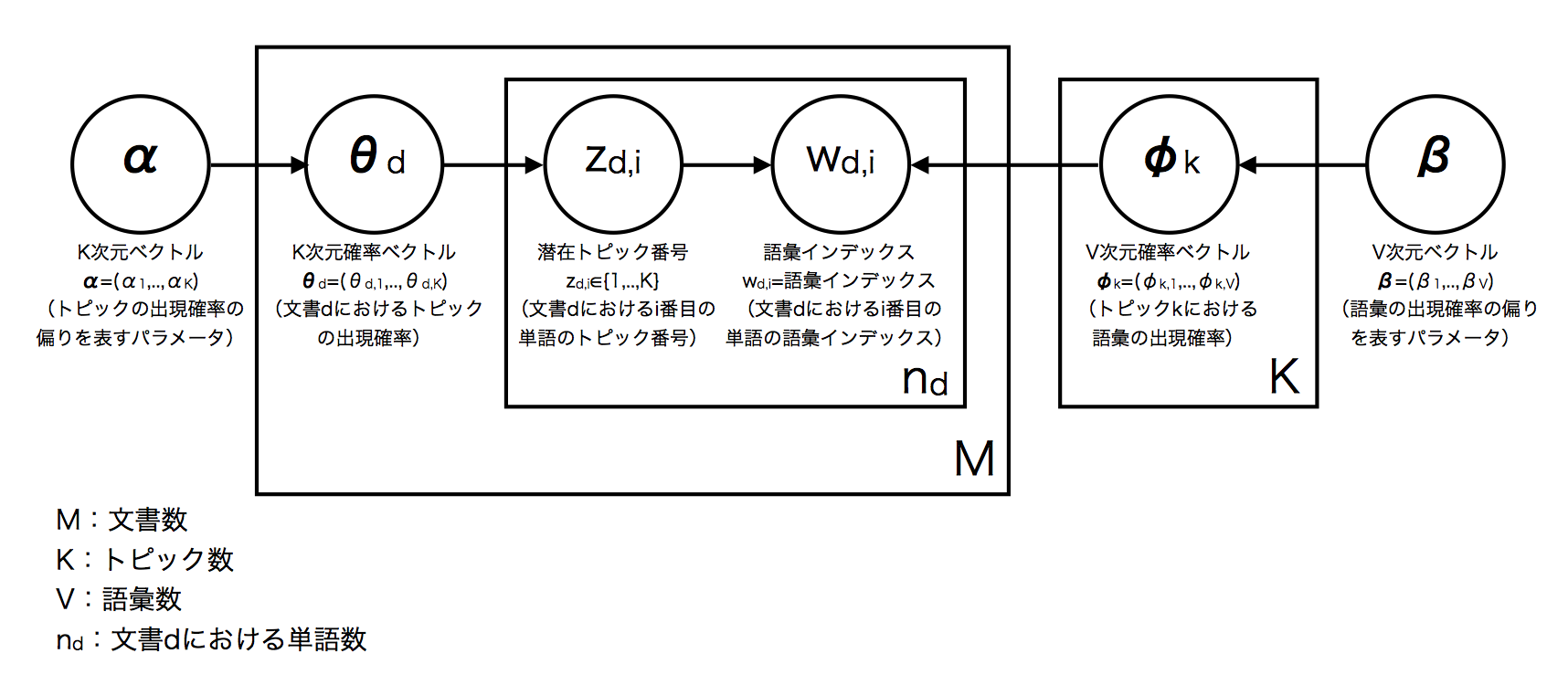
それでは、LDAのデイレクレ分布が使われてる部分を見てみましょう。LDAの各確率変数の確率分布は以下のようになります。

LDAの各変数の意味と幾何的解釈について - どこでも見れるメモ帳より引用

ここで注意したいのは下の二式です。

ϕk→∼Dir(β⃗ ) (k=1,..,K)

θd→∼Dir(α⃗ ) (d=1,..,M)

話を簡単にする為に、本記事ではϕk→∼Dir(β⃗ )だけを説明します。ϕk→∼Dir(β⃗ )のkは単語idを表します。単語に割り当てられるIDは予め順番に。例えばこんな感じです。

k = 1 スイング

k = 2 リズム

k = 3 コーヒー

k = 4 シンガー

……

k = K アルゴリズム (Kとは総単語数)

記号を見ても分かるように、ϕkはベクトルです。上の図にも書いてあるとおり、ϕkはv次元ベクトルです。そして、vはトピックの数を表します。分かりやすくする為に具体例を挙げます。ϕ1(k = 1)の場合を見てみましょう。

仮に

Φ1 = [50%, 30%, 20%] ([スポーツ, 音楽, 芸能])

とします。右の括弧はそれぞれのベクトル要素の表すトピックを示してます。

このΦ1は何を表してるかと言いますと、k = 1の単語（図13で言うとスイング）は50%の確率でスポーツというトピックに属し、30%の確率で音楽というトピックに属し、20％の確率で芸能と言うトピックに属すると言う意味なのです。Φ1の値を合計すると、勿論100%になります。このように、Φベクトルは各単語がどのくらいの確率で各トピックに割り当てられるかを表すベクトルなのです。

しかし、実際のldaの問題ではそれぞれの単語が何%の割合で各トピックに振り当てられてるかは分かりません。

確率は以下のように

Φ1 = [x1, x2, x3] ([スポーツ, 音楽, 芸能])

とブラックボックスになっております。そして、それぞれの[x1, x2, x3]を求めるのがldaの数理モデルの目的の一つなのです。

それでは、具体的にどのように求めればいいのでしょうか。ここで、例のデイレクレ分布が役に立つのです。解き方は複雑ですので、本記事では概要だけを説明しましょう。[x1, x2, x3] の変数の割り当てをデイレクレ分布に従うと仮定すればいいのです。式は以下のようになります。

前章でも話したように、デイレクレ分布は比較的融通が効く確率分布であります。ldaは具体的には沢山の文章を読みこんで、その時の度合いに応じてパラメータを更新します。もし、入ってる文章の中で単語スイングがスポーツのトピックとして沢山入ってくるのでしたら、スポーツの変数の指数であるα1を1に物凄く近い（けど1より小さい）数に変換すればいいのです。そうすれば、確率変数はx1に近づけば近づくほど確率が高くなります

。逆にk = 4の「シンガー」はスポーツではあまり出そうにない単語です。x2, x3の音楽や芸能で出てきそうな単語です。ですから、今度はα2とα3を0.8, 0.9と設定して、α1を1.1と設定すれば確率的にはスポーツ以外のトピックに集まるでしょう。

さて、余談ですが今回は「30%になる確率」とか結構メタい「確率の確率」を話しました。これが殆どの教科書で話してるデイレクレ分布は「サイコロの目の確率」の意味なのです。一般のサイコロを振ると六分の一になりますが、デイレクレ分布ではそれぞれの出る目が「六分の一」になる確率を示しているのです。

3.2.2 確率的ブロックモデル

まずは下のブロックをご覧下さい。

確率的ブロックモデルをJuliaで実装したより引用

左側の図形を右のような3x3の格子に分割できると仮定しましょう。確率的ブロックモデルとは、列や行を並べかえて、右のように指定した格子に分割する事です。格子内は。

確率的ブロックモデルは[tex:\begin{align*}
{\boldsymbol \theta}^\textit{1} &\sim {\rm Dirichlet}({\boldsymbol \alpha}^\textit{1}) \\
{\boldsymbol \theta}^\textit{2} &\sim {\rm Dirichlet}({\boldsymbol \alpha}^\textit{2}) \\
\{\{ \phi_{k\ell} \}_{\ell=1}^{L} \}_{k=1}^{K} &\sim {\rm Beta}(a_0, b_0) \\
\{ z_i^\textit{1} \}_{i=1}^{N^\textit{1}} &\sim {\rm Categorical}({\boldsymbol \theta}^\textit{1}) \\
\{ z_j^\textit{2} \}_{j=1}^{N^\textit{2}} &\sim {\rm Categorical}({\boldsymbol \theta}^\textit{2}) \\
\{\{ x_{ij} \}_{j=1}^{N^\textit{2}} \}_{i=1}^{N^\textit{1}} &\sim {\rm Bernoulli}(\phi_{z_i^\textit{1} z_j^\textit{2}})
\end{align*}
]

ここでは話を簡単にする為、具体的な解法は説明しません。単に第3行で使われてるデイレクレ分布(正確にはベータ分布)の表す意味を解説します。ここではパラメータはα、βではなくa, bとなってます。

第3行公式のlは行のクラスタを表し、kは列です。クラスタとは列、行の分類で下の図で言うと[A,B,C]がそれにあたります。確率変数の $\phi$ は連結度を表してます。連結度どは「クラスタk, lに所属する確率を表してます」。私の仮定してるクラスタは数字で表すので、[A,B,C]じゃなくて[1,2,3]と表す事にしましょう。

https://www.researchgate.net/publication/263710713_Stochastic_Blockmodeling_of_the_Modules_and_Core_of_the_Caenorhabditis_elegans_Connectome?_sg=_yrPocyvpylkxuaUQAhtGODJUDtePzKsjpWz2u65wBmcRc3q11M6KtyFT2FCqPaTzqBDTAdFow より引用

ここまでは一見普通の分布です。ところが、確率的ブロックモデルではパラメーターに追加項があります。前も話しましたが、デイレクレ分布でパラメータが1より大きい場合、aとbの小さい方にグラフが傾くと話しました。今回のケースに落としこむと、aが大きい場合、連結度が高い（ $\phi$ が大きい）確率が高くなり、逆にbが大きいと連結度が低い確率の方が高くなります。a, bを調整して、ある点が「k, l」クラスタに所属する確率を表してるのです。

付録A*

デイレクレ分布の乱数の実装は

逆変換法 (3) - 人工知能に関する断創録

（β分布）

とギブスサンプリングという手法を使います。

付録B*

さて、今回は任意のの範囲の乱数の発生の仕方を話しましょう。0~50までを例にしましょう。答は簡単です。確率変数の $\mu$ を $frac{\mu}{50}$ と元々の確率変数に分配すればいいのです。マイナスの値が欲しい時は（例えば-25から25）、 $frac{\mu + 25}{50}$ と変化させればいいのです。

$\begin{aligned} θ^{1} & \sim D i r i c h l e t (α^{1}) \\ θ^{2} & \sim D i r i c h l e t (α^{2}) \\ {{ϕ_{k ℓ}}_{ℓ = 1}^{L}}_{k = 1}^{K} & \sim B e t a (a_{0}, b_{0}) \\ {z_{i}^{1}}_{i = 1}^{N^{1}} & \sim C a t e g o r i c a l (θ^{1}) \\ {z_{j}^{2}}_{j = 1}^{N^{2}} & \sim C a t e g o r i c a l (θ^{2}) \\ {{x_{i j}}_{j = 1}^{N^{2}}}_{i = 1}^{N^{1}} & \sim B e r n o u l l i (ϕ_{z_{i}^{1} z_{j}^{2}}) \end{aligned}$ 付録C*

単体

（ここでいう）単体とは、直角座標系の基底「座標軸上にある単位ベクトル（正の方向オンリー）」を全て結んだ図形です。

例えば、二次元の単体では

二次元単体座標の基底は(0, 1), (1, 0)なので

線を結ぶと以下のようになります。

線分の式はy = -x + 1となりますので

変形して y + x = 1となります

三次元の基底は(0, 0, 1), (0, 1, 0), (0, 0, 1)

となります。それらの点を結ぶと以下のように正三角形になります。

面の公式により、単体に属する面の公式はx + y + z = 1の

四次元 (0, 0, 0, 1), (0, 0, 1, 0), (0, 1, 0, 0), (1, 0, 0, 0)になります。

距離の公式はどの次元でも変わりません。よって、4つの点の各々の距離を計算すると全て等しい事が分かります。更に、公式x1 + x2 + x3 + x4 = 1に所属するので、上の点は全て3次元空間に属する事が分かります。三次元で 4つの頂点の各々の距離が等しい図形は正四面体しかありません。よって、4次元の単体は正四面体となるのです。

先程もはなしましたが、今回も

x1 + x2 + x3 + x4 = 1となります。

5, 6, 7...と他の次元も同じようり推理する事ができます。

x1 + x2 + x3 + x4 + …. xn = 1

はn次元で成立します。